O que é Estatística Descritiva?

Para garantir que os dados coletados em campo se transformem em informações relevantes para a tomada de decisões é necessário tornar essa informação compreensível. A Estatística Descritiva é o instrumento que permite concentrar dados e os reduzir à informações.

No entanto, como acontece sempre que resumimos, a transformação dos dados em indicadores implica também na perda de propriedades. Por exemplo, podemos ter um lote com tamanho médio adequado das mudas, porém com grande quantidade de plantas fora dos padrões aceitáveis.

Este viés causado pela redução da informação a um único indicador pode ser minimizado pela utilização de várias medidas em conjunto, que nos permitam cruzar informações e compor um  mostruário de interpretações dos nossos dados. Esta é uma das razões pelas quais é importante que os dados se apresentem em relatórios de investigação terem várias mais medidas descritivas associadas. Por exemplo, o valor da Média (medida de centralidade) é frequentemente apresentado em associação com o valor do Desvio Padrão (medida de dispersão).

Existem 3 tipos de medidas, que são:

• Medidas de Centralidade
• Medidas de Dispersão
• Medidas de Distribuição

Medidas de Centralidade

Quando queremos resumir os dados de uma distribuição, utilizando apenas um número, recorremos a medidas de tendência centralidade. As principais medidas são a Média, Moda, Mediana e o Percentil.

A Média é a soma dos dados dividida pelo número de dados coletados. O valor da média não permite, porém, saber como é que se distribuem os valores  pelos diferentes dados da amostra, isto é, não nos diz qual o grau de homogeneidade da distribuição.

A Moda é o valor mais frequente numa distribuição.  Ela é útil para identificação da “normalidade” do processo, ou seja, entender o que ocorre com o dado na maioria das vezes.

A Mediana é o valor que se situa a meio da fila ordenada dos valores da nossa distribuição, desde o mais baixo ao mais alto. A mediana indica o centro da distribuição da variável, ou seja, é o valor acima do qual estão 50% dos valores da variável e abaixo os restantes 50%. A vantagem de trabalhar com a mediana é que ela desconsidera valores incomuns da operação que poderiam alterar a média (valores atípicos muito altos ou baixos, conhecidos como outliers).

O conceito da mediana pode ser generalizado para outras percentagens além dos 50%. Podemos querer saber, por exemplo, qual é o valor abaixo do qual estão 1%, 20%, 30%, ou 75% dos dados. Essa medida de posição é conhecida como Percentil. A mediana é o percentil 50 (P50). Alguns percentis têm uma designação específica. Por exemplo, os percentis 25, 50 e 75 são referidos como o 1º quartil (Q1), 2º Quartil (Q2) e 3º quartil (Q3), respectivamente.

Medidas de dispersão

Para apresentar a homogeneidade dos dados usam-se as Medidas de dispersão, que são parâmetros estatísticos usados para determinar o grau que os dados divergem dentro de um conjunto. A utilização desses parâmetros tornam a análise de uma amostra mais confiável. As principais medidas de dispersão são Amplitude, Intervalo-Interquartil, Variância, Desvio Padrão e o Coeficiente de Variação.

A Amplitude é definida como a diferença entre a maior e a menor observação de um conjunto de dados. Ela é usada para apresentar a variação máxima entre itens de um conjunto. Sua desvantagem é não levar em consideração como os dados estão efetivamente distribuídos, assim ela não é muito utilizada.

O Intervalo-Interquartil usa o mesmo conceito da amplitude, mas o aplica entre os quartis. Assim ele apresenta a variação máxima dentro dos quartis pré-determinados.

A Variância representa a dispersão das respostas numa distribuição, ou seja, a média das diferenças entre o valor de cada resposta e a média da distribuição (desvios). Como a soma de todos desvios é sempre igual a zero, esse valor deve ser elevado ao quadrado, dando um resultado não nulo, e só depois calcula-se a média. O grande problema dessa medida é que sua unidade de medida será a unidade original ao quadrado, assim sua interpretação é menos intuitiva.

Para resolver o problema das medidas da variância, deve-se calcular a raiz quadrada dela, obtendo assim o Desvio Padrão. Essa é a medida de dispersão mais utilizada.

Como o Desvio Padrão é um valor absoluto, um problema que ocorre é que somente com o seu valor é difícil de examinar se o grau de homogeneidade é baixo. Dessa forma, para entender como a variação se comporta de forma relativa aos valores normais dos dados, calculamos qual a porcentagem de variação que o desvio padrão representa. Assim multiplicamos o desvio por 100 e dividimos o resultado pela média, chegando ao Coeficiente de Variação.

Medidas de Distribuição

O conceito de distribuição é um dos mais relevantes para a Gestão da Qualidade. Toda a estatística paramétrica assenta no pressuposto de que as médias dos fatores e variáveis da população se distribuem de acordo com a distribuição normal.

Uma distribuição normal perfeita caracteriza-se pelo fato de 68.26% dos casos se concentrem em valores que se situam no intervalo entre um desvio padrão acima e um desvio padrão abaixo da média. Esse valor sobe para 95.44% quando consideramos dois desvios padrões (acima e abaixo da média) e 99.73% se considerarmos três desvios padrões. Esse conceito é a base para o 6 Sigma.

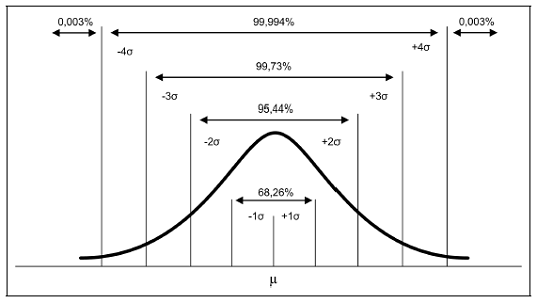
Comportamento da Distribuição Normal

Assim com os valores da média e o desvio padrão conseguimos estimar a frequência de ocorrência dos dados.

Apesar disso pode ocorrer que os dados colhidos não sigam uma curva normal perfeita, apresentando diferenças em vários aspectos. Para identificar essas diferenças utilizamos as medidas de distribuição, que são: medidas de achatamento (Kurtose) e medidas de simetria da curva de distribuição (Skewness).

A Kurtose mede o grau de achatamento da curva. As distribuições achatadas têm uma maior dispersão de valores pelos extremos da curva e as distribuições altas têm uma maior concentração de valores em torno da média (centro da curva).

A Skewness mede a assimetria das caudas da distribuição. As distribuições assimétricas são aquelas que têm um dos lados da distribuição com mais elementos que o outro (assim a média difere da mediana), enquanto as distribuições simétricas tem obliquidade igual a zero (a média é igual à mediana). Se o valor da obliquidade for maior que zero, isso quer dizer que essa distribuição tem uma lado esquerdo (valores abaixo da média) com mais elementos, se o valor for inferior a zero, então a distribuição tem o lado direito (valores acima da média) com mais elementos.

Fontes usadas:

https://www.ime.unicamp.br/~hlachos/estdescr1.pdf

https://sondagenseestudosdeopiniao.wordpress.com/estatistica/estatistica-descritiva

http://www.portalaction.com.br/estatistica-basica

https://www.fm2s.com.br/estatistica-descritiva-basica-e-centralidade

https://www.todamateria.com.br/medidas-de-dispersao/

João Victor Ribeiro Santos

Engenheiro de Produção

Coordenador do GT Qualidade Florestal