Como determinar o tamanho de uma amostra?
Um grande problema nas organizações é determinar se a coleta de dados faz ou não sentido. Caso ela seja superdimensionada a empresa está perdendo recursos. Caso ela esteja subdimensionada os dados colhidos não tem solidez o suficiente para apoiar a tomada de decisão.
Nesse contexto, quando vamos fazer as coletas de dados temos dois tipos de situação:
- A primeira é quando trabalhamos com uma quantidade total de indivíduos (população) pequena o bastante para que conseguamos mensurar todos os dados de todos indivíduos. Um exemplo disso é o salário médio de uma equipe, para o determinar basta apenas somar todos salários e dividir pelo número total de funcionários. A estatística gerada nesse caso é precisa, não há duvidas sobre seu valor. Esse tipo de dado é chamado de Parâmetro Populacional.
- Outro caso mais complexo é quando temos uma população tão grande que se torna impossível (ou inviável) a coleta dos dados de interesse de todos presentes. Dessa vez é necessário definir uma amostra e a partir dela inferir qual é o valor do parâmetro. O dado coletado nesse caso é chamado de estatística amostral.
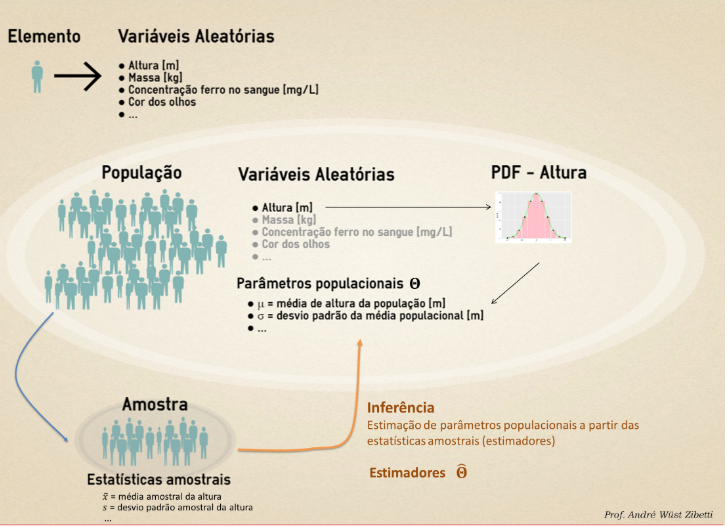
Fonte: https://www.inf.ufsc.br/~andre.zibetti/probabilidade/estimacao-de-parametros.html
Como o segundo caso é mais comum e definir a amostra não é uma tarefa simples, a presente matéria visa responder a questão:
Como fazemos para determinar uma amostra?
Em um processo que envolva amostragem o valor real do parâmetro populacional não é conhecido, apenas estimado por meio de técnicas estatísticas. Nesse caso devemos determinar o coeficiente de confiança para o dado. Quanto menor ele for menos precisa é a estimação, porém quanto maior, maior a quantidade de itens a serem coletados, o que torna maior o custo da estimação. Com esse nível é determinado um intervalo qual o dado de interesse está contido, chamado de intervalo de confiança.
A interpretação correta desse fator é em X% (nível a ser determinado) das vezes o intervalo construído a partir da amostra incluirá o verdadeiro parâmetro populacional. O coeficiente mais utilizado é 95%, ou seja, em 95% dos casos o valor do parâmetro está dentro do intervalo de determinado.
Outro ponto a ser levado em consideração é a margem de erro aceitável para a coleta de dados. Ela reflete a diferença aceitável entre o parâmetro populacional (valor real) e a estatística estimada (valor coletado). Um intervalo muito grande possui uma ótima confiança, os dados estarão dentro desse intervalo com muita frequência, porém a tomada de decisão na empresa será menos precisa. Na outra extremidade um intervalo muito pequeno onerará o processo de coleta de dados, fazendo com que a empresa faça um dispêndio exagerado de recursos.
Como regra geral amplitude de uma margem de erro não deve ser maior que de 10% do valor do dado de interesse.
Entendido esses conceitos básicos, como fazemos para determinar o tamanho da amostra?
Como exemplo usaremos o parâmetro média populacional para as contas.
Inicialmente devemos fazer uma amostragem piloto para determinar qual é a média e o desvio padrão estimados da população.
Para determinar o intervalo de confiança, numa população grande, e com uma variabilidade desconhecida (medida aqui usando o desvio padrão), usamos a equação:

Como anteriormente conceituado a margem de erro é a diferença máxima entre o valor coletado e o parâmetro populacional, logo a margem de erro (E) é:
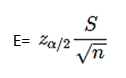
Isolando o tamanho amostral chegamos à sua equação:
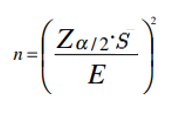
Essa fórmula é a geral e pode ser usada para calculo do tamanho da amostra.
Caso o tamanho da amostra encontrado for maior que o da amostra piloto significa que os dados colhidos inicialmente não tem solidez suficiente, dessa forma deve-se fazer novamente uma coleta preliminar e calcular o tamanho da amostra. O processo é repetido até o tamanho da amostra calculado for menor que o tamanho da amostra piloto.
Usando os valores sugeridos temos:
- O valor tabelado Z para um intervalo de confiança de 95% é 1,96.
- A margem de erro usual é 10% da média.
Assim temos:
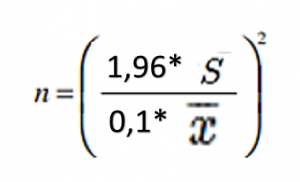
Fontes usadas:
https://www.inf.ufsc.br/~andre.zibetti/probabilidade/estimacao-de-parametros.html
http://www.cienciasecognicao.org/portal/wp-content/uploads/2011/09/Tamanho-da-Amostra-1-1.pdf
https://www.infopedia.pt/$amostra-(estatistica)
https://wikiciencias.casadasciencias.org/wiki/index.php/Par%C3%A2metro_(Estat%C3%ADstica)
 João Victor Ribeiro Santos
João Victor Ribeiro Santos
Engenheiro de Produção
Coordenador do GT Qualidade Florestal